Quadratische Funktionen

Inhalt

• Grundlegendes                                                          (Seite 1)
• Bedeutung der Parameter
• Quadratische Ergänzung
• Lösungen quadratischer Gleichungen
• Scheitelpunktform                                                     (Seite 2)
• Aufstellen quadratischer Funktionen
• Bestimmung des Scheitelpunkts                                 (Seite 3)
• ParabelRechner

Grundlegendes

Eine quadratische Funktion, oder auch Funktion 2. Ordnung genannt, ist im allgemeinen eine Funktion der Form f(x) = ax² + bx + c. Sie ist ein Polynom 2. Ordnung, denn ihre höchste Potenz ist die 2. Der Graph einer solchen Funktion heißt Parabel. Wichtig zu erwähnen ist hierbei, dass der Vorfaktor a ungleich 0 sein muss! Denn wäre a = 0 würde der Ausdruck ax² wegfallen und die Funktion wäre somit nicht mehr quadratisch, sondern linear. Die wohl einfachste und bekannteste Form einer quadratischen Funktion ist f(x) = x². Der Graph dieser Funktion heißt Normalparabel. 

Bedeutung der Parameter

Im folgenden wollen wir den Einfluss der Parameter (Koeffizienten) a, b und c auf den Graph der Funktion f(x) = ax² + bx + c untersuchen. 

Der Paramater a

Er bestimmt zunächst ob die Parabel nach oben oder nach unten geöffnet ist. Es gilt für:

• a > 0 ist die Parabel nach oben geöffnet
• a < 0 ist die Parabel nach unten geöffnet

Zudem gibt der Koeffizient a Auskunft darüber ob der Graph gestreckt oder gestaucht ist. Es gilt für:

• |a| < 1 ist der Graph gestaucht
• |a| > 1 ist der Graph gestreckt

Beispiel 1

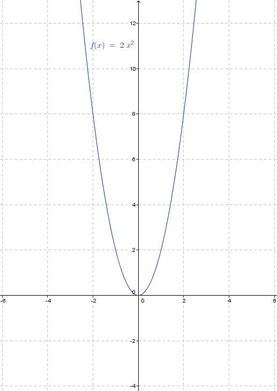
Gegeben sei die Funktion f(x) = 2x². Den Parameter a können wir einfach ablesen. Das ist einfach diejenige Zahl, die vor dem x² steht. In diesem Fall gilt also a = 2. Nun, da 2 > 0 ist, wissen wir, dass der Graph der Funktion nach oben geöffnet sein muss. Jetzt bleibt nur noch die Frage, ob die Parabel gestaucht oder gestreckt ist. Der Betrag von a, also |a|, ist 2. Deshalb gilt, da 2 > 1, dass der Graph gestreckt ist. Nachfolgend kannst du den Graph der Funktion sehen (klicke auf das Bild um es zu vergrößern). 

Beispiel 2

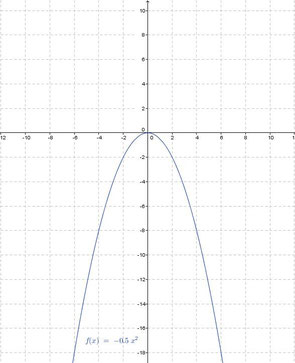
Nun betrachten wir die Funktion f(x) = -0,5 x². Den Koeffizienten a erhalten wir durch ablesen. Zu beachten ist, dass du das Vorzeichen nicht vergisst! Also a = -0,5. Da -0,5 < 0 ist, wissen wir, dass die Parabel nach unten geöffnet sein muss. Der Betrag von a, also |a|, ist |-0,5| = 0,5. Der Graph der Funktion ist also gestaucht,
denn es gilt 0,5 < 1. Nachfolgend kannst du den Graph der Funktion sehen (klicke auf das Bild um es zu vergrößern).

Der Parameter b

Er gibt die Steigung der Parabel im Schnittpunkt mit der y-Achse an. Viel mehr lässt sich hierzu auch nicht mehr sagen.

Beispiel 1

Gegeben ist die Funktion f(x) = x² + 2x. Den Parameter b können wir herauslesen. Er ist die Zahl, die vor dem x steht, also b = 2. Der Graph dieser Funktion sieht so aus (klicke auf das Bild um es zu vergrößern): 

Nun, was können wir jetzt sehen? In dem Punkt, wo die Parabel die y-Achse schneidet, hat sie die Steigung der Geraden, nämlich 3. Das ist auch eigentlich logisch, wenn wir uns dazu noch einmal die quadratische Funktion f(x) = ax² + bx + c näher anschauen. Denn in ihr steckt schließlich ein linearer Teil der Form bx + c. Und genau dieser Ausdruck bx + c sagt uns welche Steigung die Parabel im Schnittpunkt mit der y-Achse besitzt.

Beispiel 2

Gegeben sei eine Funktion der Form f(x) = x² - 2. Da in dieser Gleichung kein x steckt, gilt b = 0. Denn man könnte die Gleichung auch anders schreiben, nämlich f(x) = x² + 0x - 2. Wir wissen nun, dass die Parabel in dem Punkt wo sie die y-Achse schneidet keine Steigung hat. Dies soll dir im folgenden Bild noch einmal bewusst werden (klicke auf das Bild um es zu vergrößern). 

Der Parameter c

Er sagt aus um wie viel die Parabel in y-Richtung nach oben oder nach unten verschoben ist. Dabei gilt:

• wenn c < 0 ist die Parabel nach unten verschoben
• wenn c > 0 ist die Parabel nach oben verschoben

Dabei sollte man auf folgendes achten! Gegegeben seien folgende Funktionen

• Funktion 1: f(x) = x² + x
• Funktion 2: g(x) = x² + x + 2

Dabei können wir nun bei beiden Funktionen den Parameter c ablesen. Es folgt:

• c₁ = 0 für die Funktion 1
• c₂ = 2 für die Funktion 2

Da c₂ = 2 > 0 ist, wissen wir, dass Funktion 2 gegenüber Funktion 1 um 2 LE (Längeneinheiten) nach oben verschoben ist. Dies kannst du auch in dem folgendem Bild sehen (klicke auf das Bild um es zu vergrößern). 

Quadratische Ergänzung

Die quadratische Ergänzung ist in der Mathematik von großer Bedeutung. Hier solltest du jetzt genau aufpassen, denn dies ist ein ganz entscheidender und bedeutender Teil um eine quadratische Funktion auf Scheitelform zu bringen. Auch kann man durch quadratisches Ergänzen quadratische Gleichungen lösen, also ihre Nullstellen herausfinden.

Aber was ist denn nun diese quadratische Ergänzung? Nun im Grunde addieren wir nichts weiter als die Zahl 0 zu einer Gleichung, damit verändern wir ja nichts an der Gleichung. Ok, das ist nun ein bisschen verwirrend. Schauen wir uns die quadratische Ergänzung mal allgemein an. Wir haben eine Funktion der Form f(x) = ax² + bx + c. Der erste Schritt der quadratischen Ergänzung ist es nun die Gleichung auf Normalform zu bringen. Das heißt nichts anderes, als den Vorfaktor von x² auszuklammern, also: 

Der zweite Schritt ist nun, den Vorfaktor von x, also hier b/a, IMMER durch die Zahl 2 zu dividieren und das Ergebnis dann quadrieren. Und den erhaltenen Ausdruck addieren wir schließlich zur Gleichung, ziehen ihn jedoch auch wieder davon ab! 

Wichtig ist, dass du den Ausdruck innerhalb der eckigen Klammern addierst und wieder abziehst! Soooo und jetzt schau dir das mal genau an. Und vielleicht merkst du, dass du nun eine binomische Formel bilden kannst, nämlich: 

Zur Erinnerung: Die erste binomische Formel lautet
(a +b)² = a² + 2ab + b². Ersetzen wir dies nun, so folgt:

Beispiel 1

Gegeben sei die Funktion f(x) = 3x² + x + 9. Wende dabei das Verfahren der quadratischen Ergänzung an. 

• Schritt 1: Funktion auf Normalform bringen (das bedeutet, den Vorfaktor von x² ausklammern):

• Schritt 2: Dividiere den Vorfaktor von x, also hier 1/3, durch 2:

• Schritt 3: Quadriere nun das Ergebnis (gemeint sind die 1/6). Addiere es zu der Gleichung und zieh es wieder ab (wichtig: innerhalb der Klammern addieren/subtrahieren!):

• Schritt 4: Erkennen der binomischen Formel

• Schritt 5: Ersetze den Ausdruck a² + 2ab + b² durch (a + b)² (obige binomische Formel): 

• Schritt 6: Ausmultiplizieren, indem du alle Summanden in der eckigen Klammer mit 3 multiplizierst, also:

Beispiel 2

Gegeben sei die Funktion f(x) = -x² + 4x +3. Wende dabei das Verfahren der quadratischen Ergänzung an.

• Schritt 1: Funktion auf Normalform bringen (das bedeutet, den Vorfaktor von x² ausklammern):

• Schritt 2: Dividiere den Vorfaktor von x, also hier -4, durch 2:

• Schritt 3: Quadriere nun das Ergebnis (gemeint sind die -2). Addiere es zu der Gleichung und zieh es wieder ab (wichtig: innerhalb der Klammern addieren/subtrahieren!):

• Schritt 4: Erkennen der binomischen Formel

• Schritt 5: Ersetze den Ausdruck a² - 2ab + b² durch (a - b)² (obige binomische Formel): 

• Schritt 6: Ausmultiplizieren, indem du alle Teile in der eckigen Klammer mit -1 multiplizierst, also:

Lösungen quadratischer Gleichungen

Was meine ich mit Lösungen von quadratischen Gleichungen? Ganz einfach, damit sind die Nullstellen der Funktion gemeint. Also diejenigen x-Werte für die der dazugehörige y-Wert gleich 0 ist. Und genau darin steckt auch schon der Ansatz, denn es muss gelten:

f(x) = 0 oder hier speziell bei quadratischen Funktionen
f(x) = ax² + bx + c = 0.

Wir müssen also herausfinden, ob die Parabel Schnittpunkte mit der x-Achse hat. Schnittpunkt mit der x-Achse bedeutet immer, dass die y-Koordinate null sein muss. 

Des halb gilt, wenn nach den Schnittpunkten - und die Betonung liegt auf Punkt, das heißt es ist nach einer x und y-Koordinate gefragt - gefragt ist: SN (x|0)

Im folgenden Bild kannst du die Nullstellen einer quadratischen Funktion (gekennzeichnet durch die grünen Punkte x₁ und x₂) erkennen (klicke auf das Bild um es zu vergrößern). 

In den folgenden Beispielen, aber auch in den Übungen wird bei mir die kleinste Nullstelle immer x₁ sein, also x₁ < x₂. Dies war bei mir damals in der Schule so üblich und eigentlich ist es auch logisch, wenn du dir den Graphen oben nochmal genauer ansiehst. Dies soll dich jetzt aber nicht verwirren! Solange dein Lehrer oder deine Lehrerin nichts näher dazu festgelegt hat, kann es dir egal sein ob x₁ die kleinere oder größere Nullstelle deiner Funktion ist.

Ich werde dir als nächstes 3 Möglichkeiten vorstellen um die Nullstellen quadratischer Funktionen zu ermitteln. 

• Möglichkeit 1: Lösung mit Mitternachtsformel 
• Möglichkeit 2: Lösung mit pq-Formel
• Möglichkeit 3: Lösung mit quadratischer Ergänzung

Lösung mit Mitternachtsformel

Die Mitternachtsfomel - kurz MNF, oder auch abc-Formel genannt - ist mein Favourit quadratische Gleichungen zu lösen. Sowohl in Schule, als auch im Studium habe ich bisher immer die MNF angewandt. Sie ist ähnlich mit der pq-Formel. Die einen mögen sie lieber als die pq-Formel, die anderen wieder gar nicht. Mir persönlich ist es eigentlich ganz egal wie du die Gleichung löst, solange du sie löst und zwar richtig. Nun, sie heißt wohl Mitternachtsformel, da du sie auch um Mitternacht noch auswendig können solltest. Aber das, ganz ehrlich, dürfte doch zu schaffen sein. 

Die Mitternachtsformel einer quadratischen Gleichung der Form 
f(x) = ax² + bx + c = 0 lautet wie folgt:

Zur Erkärung: x_1,2 steht für die Nullstellen x₁ und x₂. Die Parameter können von der Gleichung abgelesen werden. Dabei möchte ich gleich erwähnen, dass der Koeffizient b die Zahl ist, die vor dem x steht, egal ob diese positiv oder negativ ist! Folgende Beispiele sollen dir helfen das Anwenden der MNF zu verstehen.

Beispiel 1

Gegegeben sei eine Funktion der Form f(x) = 2x² + 2x - 4. Berechne die Schnittpunkte mit der x-Achse.

Schnittpunkte mit der x-Achse bedeutet, dass nach den Nullstellen der Funktion gesucht wird.

• Schritt 1: Du musst also zu erst folgenden Ansatz verwenden: f(x) = 0 bwz. 

• Schritt 2: Nun müssen wir nur noch die Koeffizienten a,b und c von der Gleichung ablesen. Der Parameter a ist die Zahl, die vor dem x² steht, also hier die 2. Parameter b ist die vor dem x stehende Zahl, also die 2. Und schließich noch der Paramter c. Das ist der konstante Teil, also der Teil, in dem kein x vorkommt, also c = -4. 

• Schritt 3: Jetzt setzt du die Werte für a,b und c in die MNF ein. 

• Schritt 4: Nun kannst du dir die beiden Nullstellen x₁ und x₂ berechnen. Du solltest auf folgendene Ergebnisse kommen:

• Schritt 5: Da nach den Schnittpunkten gesucht war, d.h. nach x- und y-Koordinate, folgt:

Zeichnen wir den Graphen der Funktion sehen wir, dass wir mit unseren Nullstellen richtig liegen (klicke auf den Graph um ihn zu vergrößern).

Beispiel 2

Gegeben sei die Funktion f(x) = 1,3x² + 1,3x -15,6. Zu bestimmen sind die Schnittpunkte des Graphen mit der x-Achse (Nullstellen).

• Schritt 1: Als erstes musst du deine Funktion gleich Null setzen:

• Schritt 2: Ablesen der Parameter a,b und c aus der Gleichung. Zur Erinnerung: Der Paramter a ist die Zahl, die vor dem x² steht. Der Parameter b ist die Zahl, die vor dem x steht, der Parameter c ist dabei die Konstante (allgemeine Funktion f(x) = ax² + bx + c)

• Schritt 3: Setze nun die Werte für a,b und c in die MNF ein.

• Schritt 4: Nun kannst du dir die beiden Nullstellen x₁ und x₂ berechnen. 

• Schritt 5: Da nach den Schnittpunkten gesucht war, d.h. nach x- und y-Koordinate, folgt:

Zeichnen wir den Graphen der Funktion sehen wir, dass wir mit unseren Nullstellen richtig liegen (klicke auf den Graph um ihn zu vergrößern).

Lösung mit pq-Formel

Die pq-Formel bietet eine weitere Möglichkeit an quadratische Gleichungen zu lösen. Bei vielen Schülern bzw. Schülerinnen ist sie sehr beliebt. Ich bevorzuge trotzdem die Mitternachtsformel, aber das soll jetzt nicht von Bedeutung sein. Wenn du die pq-Formel verwenden willst, musst du deine quadratische Gleichung zu erst auf Normalform bringen! Das bedeutet, dass du sie so umformen musst, dass vor dem x² eine 1 steht. Allgemein bedeutet das, dass du deine Funktion die Form
f(x) = x² + px + q bringen musst. Erst wenn dies der Fall ist, kannst du die folgede Formel für die Berechnung der Nullstellen anwenden.

Im Folgenden werde ich mit dir zwei Beispielaufgaben durchgehen, damit dir klar wird, wie du die Formel anwenden musst. Die pq-Formel einer quadratischen Gleichung der Form f(x) = x² + px +q lautet:

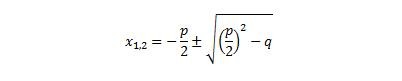
Beispiel 1

Gegeben sei eine quadratische Funktion der Form f(x) = x² + 2x -3. Berechne die Nullstellen dieser Funktion mit der pq-Formel. 

• Schritt 1: Als erstes musst du deine Funktion gleich Null setzen:

• Schritt 2: Bringe die Funktion auf Normalform [f(x) = x² + px +q]. Bei diesem Beispiel ist dies bereits der Fall, denn vor dem x² steht die 1. Also können wir sie auch so lassen:

• Schritt 3: Nun kannst du die Parameter p und q von der Gleichung ablesen, wobei p jene Zahl ist, die vor dem x steht und q die Konstante ist. Du solltest folgende Werte ablesen:

• Schritt 4: Setze jetzt die oben abgelesenen Werte in die pq-Formel ein:

• Schritt 5: Nun kannst du dir die beiden Nullstellen x₁ und x₂ berechnen.

Somit liegen die beiden Schnittpunkte bei 

Beispiel 2

Gegeben sei eine Funktion f = 2x² - 3x + 1. Bestimme die Nullstellen anhand der pq-Formel.

• Schritt 1: Als erstes musst du deine Funktion gleich Null setzen:

• Schritt 2: Bringe die Funktion auf Normalform [f(x) = x² + px +q]. Das bedeutet: Teile deine Gleichung durch jene Zahl, die vor dem x² steht, also hier die 2 (Teile jede Zahl in der Gleichung durch 2). Also folgt:

Nun haben wir die Funktion auf Normalform gebracht, denn vor dem x² steht jetzt (gedanklich) eine "1".

• Schritt 3: Nun kannst du die Parameter p und q von der Gleichung ablesen, wobei p die Zahl ist, die vor dem x steht und q die Konstante ist (die Zahl ohne x). Du solltest folgende Werte ablesen:

• Schritt 4: Setze jetzt die oben abgelesenen Werte in die pq-Formel ein:

• Schritt 5: Nun kannst du dir die beiden Nullstellen x₁ und x₂ berechnen.

Somit liegen die beiden Schnittpunkte des Graphen mit der x-Achse bei

Seite 1 | Seite 2 | Seite 3 | ParabelRechner