Lineare Funktionen

Inhalt

• Grundlegendes
• Zeichnen von Geraden
• Aufstellen einer Geradengleichung
• Lösungsverfahren zu linearen Gleichungssystemen
• Lage zweier Geraden

Grundlegendes

Bei linearen Funktionen handelt es sich um Funktionen der Form

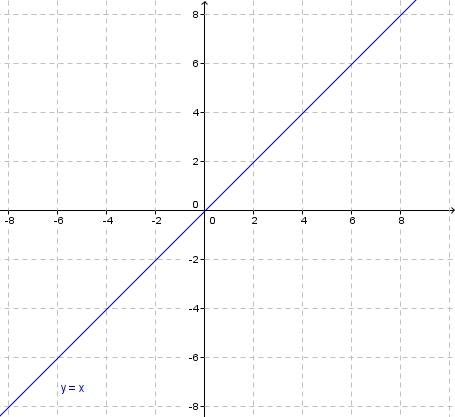
Den Graph einer derartigen Funktion bezeichnet man als Gerade. Wie ein Graph einer solchen Funktion aussehen könnte, siehst du im folgenden Bild. 

Aber nun mehr zur Geradengleichung y = mx + t (y wird auch oft mit f(x) angegeben, das ist das gleiche, keine Sorge ;-) ). 

m - die Steigung einer Geraden

m gibt die Steigung einer Geraden an, das bedeutet, wie stark oder schwach eine Gerade steigt oder fällt. Die Steigung m ist nichts anderes als ein Verhältnis einer zurückgelegten Strecke in y-Richtung zu einer bestimmten Strecke in x-Richtung. Oder einfach kurz gesagt:

Dieses kleine Dreieck Δ vor dem y oder x bezeichnen wir als "Delta" (griechischer Buchstabe). Es gibt eine Differenz zwischen zwei Werten an. Die Steigung m ist also nichts anderes als ein Streckenverhältnis. 

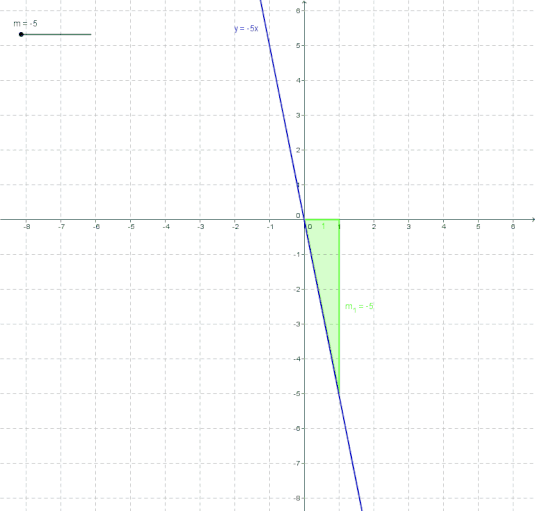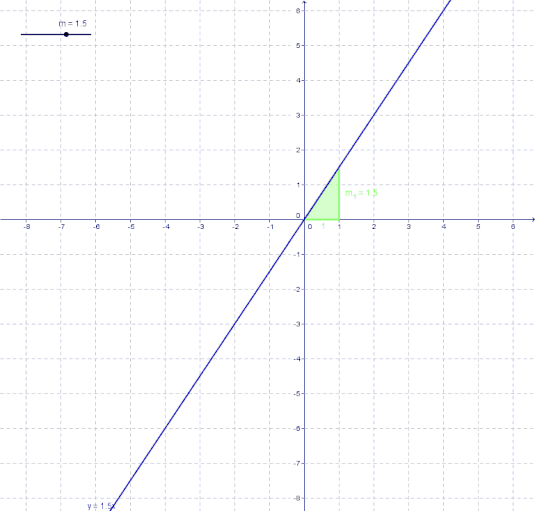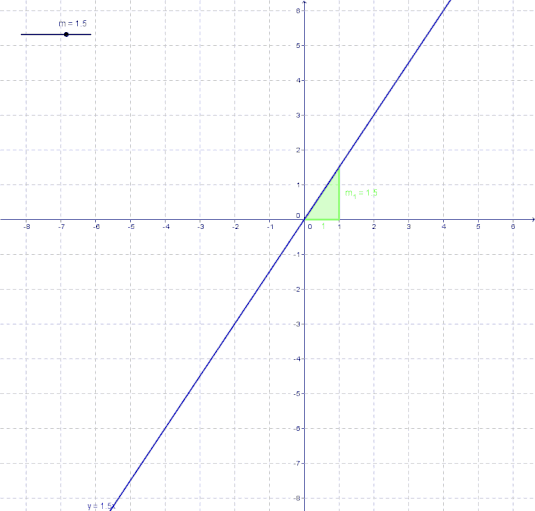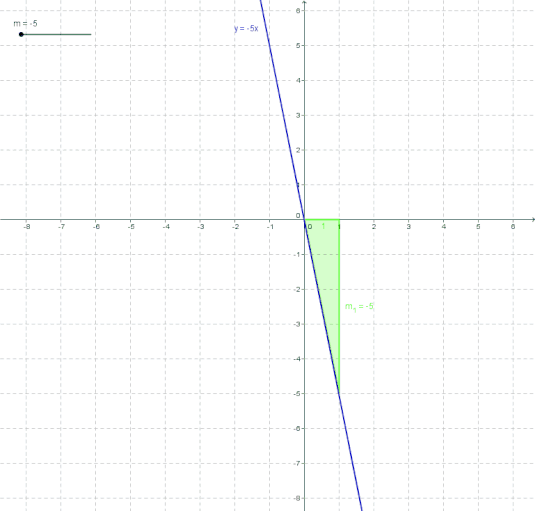
In der folgenden Animation kannst du beobachten wie der Graph für 

• m < 0 
• m > 0

aussieht.

Nun, wie kann man aber nun diese Steigung ermitteln, wenn sie nicht gegeben ist? Das schauen wir uns am Besten mal an 2 Beispielen an. 

Beispiel 1

Gegeben sei folgender Graph. Zu bestimmen ist die Steigung der Geraden. (Klicke auf das Bild um es zu vergrößern)

Wie gehen wir nun am Besten vor? Wir könnten  ein Steigungsdreieck in die Gerade zeichnen, das könnte dann in etwa so aussehen:

Im Prinzip ist es natürlich ganz egal, wo du das Steigungsdreieck und wie klein oder groß du es einzeichnest. Wichtig ist, dass die Seiten des Dreiecks Δx und Δy zu den jeweiligen Koordinatenachsen parallel sein müssen! Alles was du jetzt noch tun musst, ist mit einem Lineal die Strecken Δx und Δy zu messen und dir die Längen der Strecken notieren. Das machen wir doch gleich mal. 

Unsere Messung mit dem Lineal hat also folgende Werte ergeben:

• Δy = 6
• Δx = 4

Somit können wir die Werte in obige Steigungsformel eintragen:

Somit wissen wir, dass die gesuchte Steigung der Geraden m = 1,5 beträgt.

Dies hätte man auch noch ein wenig anders lösen können. Man sucht sich einfach zwei Punkte, die auf der Geraden liegen und liest dabei x- und y-Koordinaten der Punkte ab. In etwa so:

Lesen wir die die Koordinaten der Punkte ab (Schnittpunkte der gestrichelten Linien mit den Koordinatenachsen), so kommen wir auf folgende Werte.

• Punkt C: x-Koordinate = 8 = x₂ | y-Koordinate = 12 = y₂
• Punkt A: x-Koordinate = 4 = x₁ | y-Koordinate = 6 = y₁

 Jetzt müssen wir nur noch die Werte in folgende Formel einsetzen:

Auch mit dieser Methode kommen wir auf das Ergebnis m = 1,5.

Beispiel 2

Gegeben sei folgender Graph. Zu bestimmen ist die Steigung der Geraden. (Klicke auf die Bilder um sie zu vergrößern)

Das ganze gehen wir am Besten wie bei der vorherigen Aufgabe an, als erstes zeichnen wir uns ein Steigungsdreieck ein. Ich habe das mal so gemacht:

So, das hätten wir geschafft. Lineal her, los geht's. Messe wie die Strecken Δx und Δy ab, und notiere dir die Längen. Ich komme auf folgende Werte:

• Δx = 8
  
• Δy = 4
  

Jetzt müssen wir die Werte nur noch in die Steigungsformel einsetzen:

Somit wissen wir, dass die gesuchte Steigung der Geraden m = 0,5 beträgt.

Oder: Man sucht sich zwei Punkte, die auf der Geraden liegen und liest dabei x- und y-Koordinaten der Punkte ab:

Lesen wir die die Koordinaten der Punkte ab (Schnittpunkte der gestrichelten Linien mit den Koordinatenachsen), so kommen wir auf folgende Werte.

• Punkt C: x-Koordinate = 12 = x₂ | y-Koordinate = 6 = y₂
• Punkt A: x-Koordinate = 4 = x₁ | y-Koordinate = 2 = y₁

 Jetzt müssen wir nur noch die Werte in folgende Formel einsetzen:

t - der y-Achsenabschnitt

t bezeichnet man als den sogenannten y-Achsenabschnitt. Dies bedeutet anders gesagt: t ist die y-Koordinate des Schnittpunkts einer Geraden mit der y-Achse. Wie sich eine Gerade in Abhängigkeit von t ändert kannst du in der folgenden Animation beobachten.

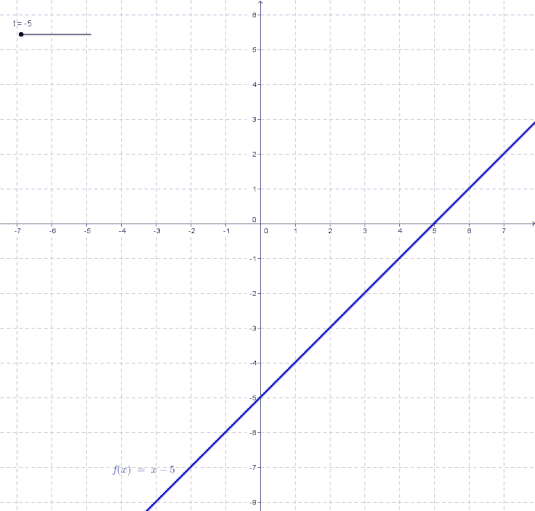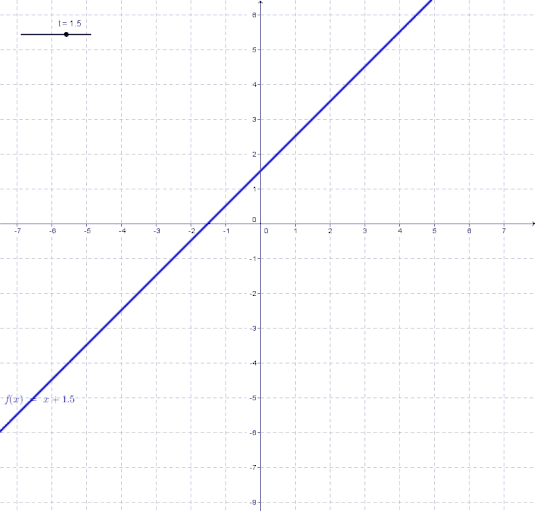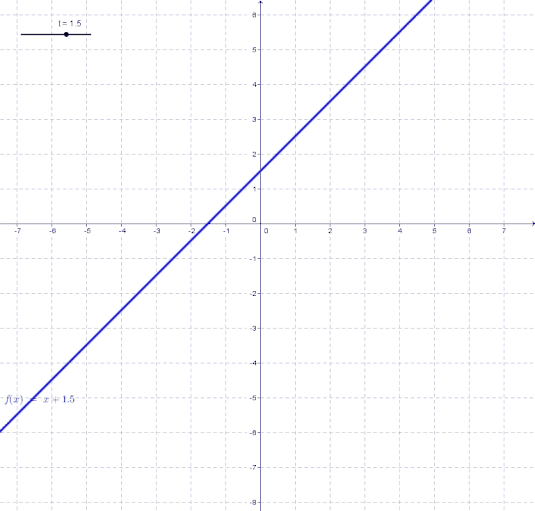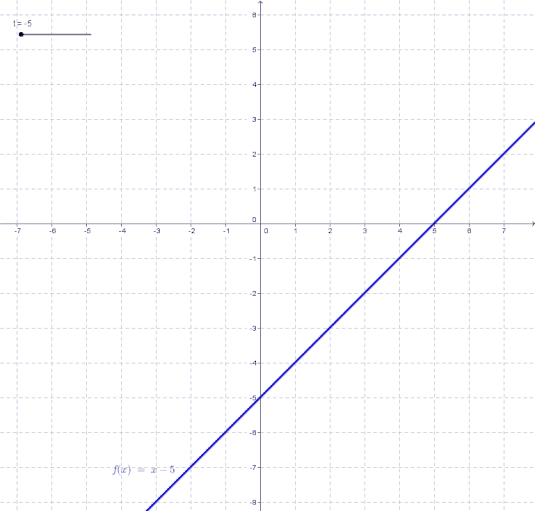
Dies wollen wir kurz an 2 Beispielen verdeutlichen. 

Beispiel 1

Gegeben sei folgende Geradenfunktion. 

Vergleichen wir diese Gleichung mit der allgemeinen Geradengleichung y = mx + t so können wir t einfach ablesen. Es folgt t = 2. 

Das ganze lässt sich auch noch graphisch verdeutlichen:

Im Graphen können wir das ganze auch schön sehen, denn die Gerade schneidet die y-Koordinate bei y = 2, was unser y-Achsenabschnitt ist. 

Beispiel 2

Gegeben sei folgende Funktion einer Geraden:

Auch hier können wir sofort wieder t ablesen. Es gilt t = -1. Jetzt frägst du dich, wieso ausgerechnet t = -1 und nicht t = +1 ein? Nun betrachten wir die Geradengleichung noch einmal ein bisschen genauer.

Die allgemeine Geradengleichung lautet y = mx + t  Also muss t = -1 sein. Der folgende Graph der Funktion wird das ganze nochmal aufzeigen.

Auch hier kann man schön erkennen, dass die Gerade die y-Achse bei
y = -1 schneidet, folglich ist der y-Achsenabschnitt t = -1.

Steigungswinkel einer Geraden

Als Steigungswinkel einer Geraden bezeichnen wir denjenigen Winkel, der zwischen x-Achse und Gerade liegt. Gemessen wird dabei gegen den Uhrzeigersinn, also von x-Achse zu Gerade. Ist der Steigungswinkel positiv, so steigt die Gerade, ist er hingegen negativ, so fällt die Gerade. 

Nun gibt es folgenden Zusammenhang zwischen dem Steigungswinkel α und der Steigung m einer Geraden:

Und warum das so ist lässt sich ganz schnell zeigen. Zu Beginn möchte ich dir sagen, dass du dich dafür im Bereich Trigonometrie (Sinus, Cosinus & Tangens) auskennen solltest. Dazu schauen wir uns am besten nochmal unser Steigungsdreieck an.

Hier haben wir also ein rechtwinkliges Dreieck, mit dem Steigungswinkel, den wir nun mithilfe einer Winkelfunktion bestimmen wollen. Vielleicht erinnert sich ja der eine oder andere zurück und kennt bereits diese Formel:

Um nun den Winkel α bestimmen zu können müssen wir die Gleichung wie folgt umformen. 

Was ist denn nun bitte dieses arctan? arctan steht für arcustangens und ist die Umkehrfunktion des Tangens. Auf dem Taschenrechner findest du diese Funktion mit folgender Abkürzung tan^-1. 

Beispiel 1

Gegeben sei die Funktion 

Zu bestimmen ist der Schnittwinkel mit der x-Achse. 

Wie du oben eben gelesen hast berechnet sich der Steigungswinkel einer Geraden mit α = arctan(m). m können wir aus der gegebenen Gleichung einfach herauslesen, das ist nämlich die Zahl die vor dem x steht, also gilt: m = 2.

Somit folgt für den Steigungswinkel α:

Um das ganze nochmal zu verdeutlichen betrachten wir kurz den Graphen der gegebenen Funktion. Wir sehen, dass wir mit α = 63,4° richtig gelegen sind. Zur Erinnerung: Der Winkel wird - entgegen dem Uhrzeigersinn - von der x-Achse zur Geraden gemessen.

Beispiel 2

Gegeben sei die Funktion

Zu bestimmen ist der Schnittwinkel mit der x-Achse. 

Wie du oben eben gelesen hast berechnet sich der Steigungswinkel einer Geraden mit α = arctan(m). m können wir aus der gegebenen Gleichung einfach herauslesen, das ist nämlich die Zahl die vor dem x steht, also gilt: m = -1.

Somit folgt für den Steigungswinkel α:

Nun haben wir einen negativen Steigungswinkel herausbekommen, was bedeutet, dass unsere Gerade fällt. In diesem Fall würde der Winkel jedoch im Uhrzeigersinn verlaufen. Da wir uns vorher aber geeinigt hatten, dass der Steigungswinkel immer gegen den Uhrzeigersinn angetragen werden sollte, müssen wir noch folgenden Zwischenschritt berücksichtigen:

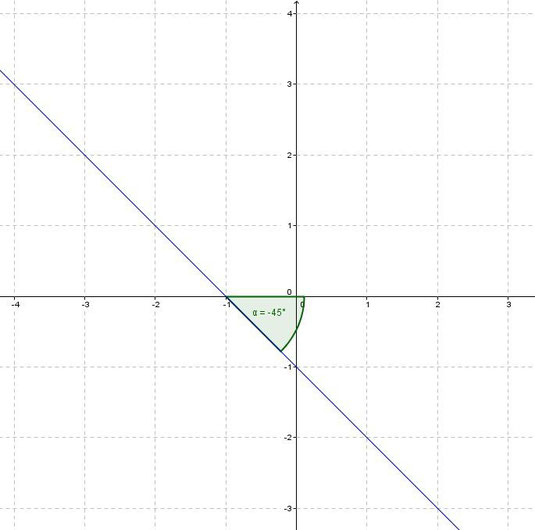
Um das ganze nochmal zu verdeutlichen betrachten wir kurz den Graphen der gegebenen Funktion. Wir sehen, dass wir mit α = -45° richtig gelegen sind. Zur Erinnerung: Der Winkel wird - entgegen dem Uhrzeigersinn - von der x-Achse zur Geraden gemessen, also folgt für den eigentlichen Steigungswinkel α' = 135°.

Generell kann man für negative Steigungen (m<0) folgende Formel für den Steigungswinkel α' aufstellen: 

wobei |α| der Betrag des negativen Steigungswinkels ist.