Flächenberechnung
Inhalt
Grundlegendes
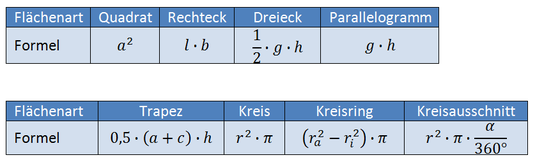
Eine Fläche ist ein Gebiet, das von allen Seiten eingegrenzt wird. Beispiele für Flächen sind das Quadrat, das Dreieck, der Kreis und vieles mehr. Der Flächeninhalt A ist ein Maß für die Größe einer Fläche. Der Umfang U einer Fläche ist die Summe all ihrer Seitenlängen.
Quadrat
Ein Quadrat ist ein Viereck mit 4 gleich langen Seiten und 4 gleich großen Innenwinkeln (90°). Der Flächeninhalt eines Quadrats errechnet sich aus dem Produkt seiner Seitenlängen.

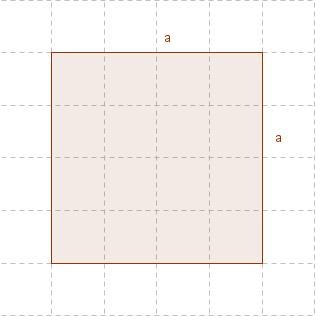
Beispielaufgabe
Ein Quadrat hat die Seitenlänge a = 4 cm. Berechne Umfang und Flächeninhalt dieses Quadrates.
Lösung:
- Umfang
Der Umfang eines Quadrates berechnet sich aus der Summe aller Seitenlängen des Quadrats.

Da die Seitenlänge des Quadrats a = 4 cm lang ist, müssen wir für a nun nur noch 4 cm einsetzen um auf den Umfang des Quadrats zu kommen. Für a = 4 cm folgt also:

- Flächeninhalt
Der Flächeninhalt eines Quadrates ergibt sich aus dem Quadrat seiner Seitenlänge.

Setzen wir nun den Wert der Seitenlänge a = 4 cm in obige Gleichung erhalten wir:

Der Flächeninhalt des Quadrats beträgt also 16 cm2.
Bemerkung: Dass Flächeninhalt und Umfang den gleichen Wert besitzen ist hier nur Zufall! Dies ist nicht immer der Fall!
Rechteck
Ein Rechteck ist ein Viereck mit 4 gleich großen Innenwinkeln (90°). Der Flächeninhalt eines Rechtecks ergibt sich aus dem Produkt seiner Seitenlängen l und b.


Beispielaufgabe
Ein Rechteck hat eine Länge von l = 9 cm und eine Breite von b = 4 cm. Gesucht sind Umfang und Flächeninhalt des Rechtecks.
Lösung:
- Umfang
Der Umfang eines Rechtecks berechnet sich aus der Summe aller seiner Seitenlängen. Also:

Diese Gleichung lässt sich nun noch ein klein wenig zusammenfassen, indem wir die 2 ausklammern. Dieser Schritt ist aber nicht zwingend notwendig.

Nun müssen wir in diese Gleichung nur noch die Werte für l und b einsetzen. Da l = 9 cm und b = 4 cm gilt, folgt:

Der Umfang des Rechtecks beträgt also 26 cm.
- Flächeninhalt
Der Flächeninhalt eines Rechtecks ergibt sich aus dem Produkt seiner Seitenlängen l und b.

Setzen wir nun die Werte für l und b ein erhalten wir:

Der gesuchte Flächeninhalt des Rechtecks beträgt also 36 cm2.
Dreieck
Ein Dreieck besitzt 3 Seiten und 3 Ecken. Die Summe aller Innenwinkel eines Dreiecks ergibt 180°. Den Flächeninhalt eines Dreiecks kann man ähnlich wie den eines Rechtecks berechnen. Denn teilt man ein Rechteck an seiner Diagonale erhält man 2 Dreiecke. Schließlich lässt sich folgern, dass die Fläche eines dieser beiden Dreiecke nur halb so groß ist wie die des zerteilten Rechtecks. Also:

Wie sich die Fläche eines Rechtecks errechnet haben wir bereits oben durchgenommen. Diese ergibt sich aus dem Produkt seiner beiden Seitenlängen, der Grundlinie g und der Höhe h. Dabei ist wichtig, dass die Höhe h senkrecht zur Grundlinie g stehen muss. Die Höhe eines Dreiecks ist also nichts weiter als die Länge einer Strecke, die auf der Grundlinie senkrecht steht und bis zur gegenüberliegenden Ecke verläuft. Somit ergibt sich folgende Formel für den Flächeninhalt eines Dreiecks.


Beispielaufgabe
Die Höhe eines Dreiecks beträgt 5 cm (1. Seite). Seine Grundlinie ist 9 cm lang (2. Seite). Die 3. Seite des Dreiecks misst 10,3 cm. Berechne den Umfang und Flächeninhalt des Dreiecks.
Lösung:
- Umfang
Der Umfang eines Dreiecks berechnet sich aus der Summe seiner drei Seitenlängen. Dabei ist beispielsweise die Höhe die erste Seitenlänge S1 und die Grundlinie die zweite Seitenlänge S2. Somit ergibt sich folgende allgemeine Formel:

Nun müssen wir nur noch die angegebenen Werte einsetzen. Mit h = 5 cm, g = 9 cm und S3= 10,3 cm folgt für den Umfang des Dreiecks:

Der Umfang des Dreiecks beträgt somit 24,3 cm.
- Flächeninhalt
Der Flächeninhalt eines Dreiecks errechnet sich aus:

Setzt man jetzt noch die Werte für g und h ein erhält man den gesuchten Flächeninhalt des Dreiecks.

Der Flächeninhalt des Dreiecks beträgt somit 22,5 cm2.
Parallelogramm
Ein Parallelogramm ist ein Viereck mit jeweils 2 zueinander parallelen, gegenüberliegenden Seiten. Zudem sind die gegenüberliegenden Seiten gleich lang, sowie die gegenüberliegenden Winkel gleich groß. Die Summe aller Innenwinkel eines Parallelogramms ist 360°. Zerteilt man ein Parallelogramm geschickt, so erhält man ein Rechteck. Die Höhe h eines Parallelogramms steht immer senkrecht auf der Grundlinie g. Somit lautet die Formel für den Flächeninhalt eines Parallelogramms:


Trapez
Das Trapez ist ein Viereck mit zwei parallelen, gegenüberliegenden Seiten a und c. Die Summe aller Innenwinkel eines Trapez ergibt 360°. Die Höhe h steht auf beiden parallelen, gegenüberliegenden Seiten senkrecht. Der Flächeninhalt eines Trapez lässt sich nach folgender Formel berechnen:



π (ausgesprochen - "pi") ist dabei eine Konstante. Sie wird auch als Kreiszahl bezeichnet. π ist eine irrationale Zahl und endet somit nie. Sie hat den Wert π = 3,14159... . Sie beschreibt das Verhältnis zwischen Kreisumfang und Durchmesser D des Kreises. Der Kreisumfang berechnet sich somit wie folgt:


Kreisring
Der Flächeninhalt eines Kreisrings ist nichts weiter als die Differenz der Flächeninhalte zweier Kreise. Dabei hat Kreis 1 den Radius ra (Außenradius des Kreisrings) und Kreis 2 den radius ri (Innenradius des Kreisrings). Kreis 1 ist dabei der größere von beiden. Somit lässt sich die folgende Gleichung aufstellen:

Setzt man nun die oben genannte Formel für den Flächeninhalt eines Kreises ein, so folgt:

Durch ausmultiplizieren der Konstanten π lässt sich der obige Ausdruck etwas kürzer darstellen.


Kreisausschnitt
Ein Kreisausschnit - auch Kreissektor genannt - ist eine Teilfäche von einem Kreis. Diese Fläche wird durch den Kreisbogen und 2 Kreisradien begrenzt. Ein Tortenstück ist beispielsweise ein Kreisausschnitt. Um den Flächeninhalt des Kreissektors zu berechnen braucht man den Winkel den die beiden Kreisradien einschließen. Ist dieser gegeben, so gilt für den Flächeninhalt:


Kommentar schreiben
tarot (Montag, 28 November 2016 15:33)
ufijczyk
sekstel (Dienstag, 29 November 2016 22:05)
sieciechowski
love spells (Mittwoch, 30 November 2016 15:58)
dagoba
love spell (Donnerstag, 01 Dezember 2016 02:10)
pokrążyć
uroki miłosne (Dienstag, 13 Dezember 2016 21:30)
quarters